Symbolic Regression
In a previous post, I looked at Gaussian process regression. Gaussian processes are powerful.They give you useful error bounds. However, often the results look like curve fitting similar to fitting with splines and I suspect that people have a difficult time interpreting the covariance kernel. Often what people want is a simple interpretation of the data. This is relatively easy if it looks like there is a linear relationship among the data or the data can be transformed to be somewhat approximately linear. Just crank up your favorite linear or generalized linear modeling (GLM) software. The software will fit the model to the data and give you the appropriate coefficients. Since the models are simple, interpretation is easy (well, maybe relatively easy). If the relationships among the data are non-linear, there's software to fit non-linear models, assuming you can come up with an appropriate set of functions to fit the data.
Suppose you don't have strong feeling for how the underlying process is generating the data, but you would still like to find a simple relationship among the variables. You could try a bunch of different models and choose the one giving the most satisfactory fit. That's the basic idea behind symbolic regression (SR). In symbolic regression, you search the space of mathematical expressions for an expression that does a reasonable job of fitting the data. Instead of assuming a functional form for the final model, you choose a set of building blocks such as operators, functions, and constants and join them in various combinations until you get a reasonable fit to the data. SR tries to not only find the parameters of the model, but also the model's structure. The end result, if we're lucky, is a model that is both accurate and interpretable by humans.
Obviously, just jamming functions together with some uniformly random scheme isn't likely to work. Combining a handful of function and operators with some constants can result in a very large space of possible functions to search. This plus the fact that there are a very large number of different models that will fit the data to the same degree means that an effective method of generating test functions is needed.
The most common techniques used in symbolic programming are evolutionary algorithms. Evolutionary algorithms such as genetic programming (GP, not to be confused with Gaussian processes) use mechanisms inspired by biology. Programs, i.e. combinations of functions, are encoded in a tree structure, similar to Lisp functions. Each internal node is a function or operator (same thing actually). Terminal nodes are constants or variables. A collection of programs is generated and the fitness of each is evaluated. In symbolic regression, fitness is typically the sum of the square difference between the function values and the data (lower values are more fit) or the data likelihood (higher values are more fit). A subset of the population is selected by fitness and genetic operators are applied. The genetic operators are operations such as crossover and mutation. In crossover, two trees are selected and selected branches from each of the trees are exchanged to produce new child trees. Mutation can change individual nodes or delete or add branches within a tree. Individuals with lower fitness are replaced by new individuals. The average fitness of the populations should increase as the algorithm proceeds. The choices of how to select individuals and how the operators are applied are the key elements for producing effective genetic programs.
I decided to try DEAP on a toy problem. I generated some data from the following simple equation
\[y = {e^{ - 2.3x}}\cos (2\pi x) + \varepsilon \]
$\varepsilon \sim {\rm N}(0,0.05)$ represents the noise in the data. The data can be generated by
Here's what the data looks like
The green line is $y = {e^{ - 2.3x}}\cos (2\pi x)$
I'll try and fit this data by minimizing the sum of squared differences between the data and the predicted function.
\[\sum\limits_{i = 1}^N {{{\left( {f({x_i}) - {y_i}} \right)}^2}} \]
${f({x_i})}$ is the value of the function generated by the GP at $x_i$.
I tried a simple GP approach to finding a fit to this toy problem. Of course, if I know that it was generated from an exponential multiplied by a cosine, I could just fit the parameters with some sort of optimization routine. Instead, I'll use DEAP to try and fit the data.
DEAP has a number of modules for creation and manipulation of objects for genetic programming. To begin, the modules are imported.
The first thing DEAP requires is to set the operators and function you want the GP to use. We will want standard operators for +. -, *, and /. Since the data looks like it might have some sort of declining exponential and a wiggle, exponential and sinusoidal function would be useful. I realize I'm cheating because I know where the data came from.
Division and exponentiation cause problems because they can both have numerical difficulties. Instead of direct division and exponent functions, I use "safe" versions to avoid over and underflow.
pset stands for primitive set. It contains the basic operations and variables. for the genetic program. The addEphemeralConstant method allows the evolutionary algorithm to define constant values. renameArguments is syntactic sugar so that "x' is printed as a variable rather than some generated label like ARG0. I'm using a general except catchall for exception because I was having trouble catching specific exceptions from DEAP.
Next, DEAP expects some details about the objects we will be operating on. The code below creates an individual object type and describes the selection, mating, and mutation operations.
genHalfAndHalf is an initialization operator. Half the time it creates an a tree where each leaf is at the same depth between min and max and the rest of the time the trees can have different heights. The population is a list of primitiveTrees. Selection is performed by a tournament. tourn_size individuals are randomly selected and the most fit individual is selected for a new generation. This process is repeated until a new population is created. Mating will be performed by crossover. A subtree is selected at random in each of two individual and the subtrees are exchanged between individuals. Mutation is accomplished by selecting a point in a tree and replacing it by a new subtree. DEAP provides a number of other selection, mutation, and initialization operators.
To get started, a population is created and the fitness of the initial population is evaluated.
The fitness criteria is the sum of the squares of the differences between an individual's tree evaluated at some point x and the value of the data at that point. The goal of the genetic program is to minimize this difference.
The compile method compiles the tree into a function. evalFunc evaluates the function at each point and returns a list.
Once the initial population is created. for each generation a new set of offspring are created and then crossover and mutation operators are applied.
Iterate for many generations and save the most fit individual over all generations.
That's it. You can get details of the various function at the DEAP website.
sDiv(mul(cos(sDiv(mul(mul(x, add(sub(cos(x), cos(sDiv(cos(cos(2)), sin(x)))), mul(cos(sub(sDiv(sDiv(neg(0.12084912071888843), cos(sin(sDiv(x, -0.6660501457462384)))), cos(sDiv(neg(sDiv(x, 1)), 1))), cos(sDiv(cos(mul(sDiv(x, -0.6660501457462384), sDiv(sDiv(sDiv(x, 1), cos(1.2208766195941578)), -0.4776167792855315))), mul(cos(1.8383603594526816), add(cos(sub(sDiv(x, -2.325902947790879), mul(x, x))), sub(cos(mul(2.4815364875941714, x)), 2.4815364875941714))))))), mul(mul(cos(sDiv(x, mul(cos(add(x, -1)), sub(x, 2.4815364875941714)))), mul(sDiv(-2.591707483553813, mul(sDiv(x, -0.6660501457462384), sDiv(sDiv(x, cos(sDiv(2.5453722898427715, 2.0823738927195503))), -0.4776167792855315))), cos(sDiv(sDiv(x, 0.34441264096461577), -0.4776167792855315)))), sub(x, sub(sin(sub(x, sub(sin(sDiv(x, cos(x))), x))), x)))))), -2.040730964037179), -0.4776167792855315)), mul(-0.0713284456494847, sDiv(1.1186438660288207, sub(sDiv(2.5453722898427715, 2.0823738927195503), sub(cos(sub(cos(-2), cos(sDiv(cos(sDiv(x, sub(sub(cos(add(x, sDiv(2.293956696850212, -2))), 2.4815364875941714), sDiv(-2, x)))), mul(cos(1.8383603594526816), add(add(cos(x), 0), sub(cos(sDiv(0, sub(x, 2.4815364875941714))), 2.4815364875941714))))))), sub(cos(sDiv(sDiv(sin(sDiv(sDiv(x, sexp(-2.7190559409962396)), -0.4776167792855315)), cos(sDiv(sDiv(add(sin(x), -1), cos(sDiv(2.5453722898427715, 2.0823738927195503))), -0.4776167792855315))), add(sin(sDiv(x, neg(x))), -1))), 2.4815364875941714)))))), x)
This result isn't especially satisfying. The fit is bad and it's unlikely that a human would come up with such a function or find it meaningful. We need some bloat control. Setting a limit on the size of the trees helps.
A second problem that arises is that the solutions in any generation tend to form large niches, i.e. many individuals have the same structure and fitness. Setting a limit on the size of a niche improves the diversity of the population and helps prevent the algorithm from getting stuck.
Limiting the tree size to six and the niche size to ten produces this fit with a sum of squares of 0.259.
Here's the equation of the red line. It's still complex.
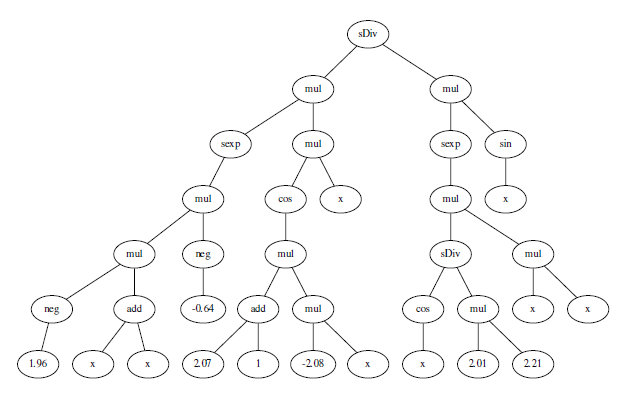
sDiv(mul(sexp(mul(mul(neg(1.9564587657410835), add(x, x)), neg(-0.6358719041262324))), mul(cos(mul(add(2.068803256811913, 1), mul(-2.0819261756570517, x))), x)), mul(sexp(mul(sDiv(cos(x), mul(2.010875005950206, 2.2109953152893054)), mul(x, x))), sin(x)))
Here's what the tree looks like
Some the subrees can be consolidated. For example add(2.07, 1) can obviously be replaced by a node a single node 3.07.
This still isn't completely satisfying, but there are many other things to try including better mutation and selection operations (DEAP has a number of them) and running several populations in parallel. I could try adding a complexity or smoothness penalty to the fitness function.
DEAP has a number of complete algorithms that make programming genetic programs easier, but I wanted to be able to experiment and see the details.
The full source code and data is available here.
Suppose you don't have strong feeling for how the underlying process is generating the data, but you would still like to find a simple relationship among the variables. You could try a bunch of different models and choose the one giving the most satisfactory fit. That's the basic idea behind symbolic regression (SR). In symbolic regression, you search the space of mathematical expressions for an expression that does a reasonable job of fitting the data. Instead of assuming a functional form for the final model, you choose a set of building blocks such as operators, functions, and constants and join them in various combinations until you get a reasonable fit to the data. SR tries to not only find the parameters of the model, but also the model's structure. The end result, if we're lucky, is a model that is both accurate and interpretable by humans.
Obviously, just jamming functions together with some uniformly random scheme isn't likely to work. Combining a handful of function and operators with some constants can result in a very large space of possible functions to search. This plus the fact that there are a very large number of different models that will fit the data to the same degree means that an effective method of generating test functions is needed.
The most common techniques used in symbolic programming are evolutionary algorithms. Evolutionary algorithms such as genetic programming (GP, not to be confused with Gaussian processes) use mechanisms inspired by biology. Programs, i.e. combinations of functions, are encoded in a tree structure, similar to Lisp functions. Each internal node is a function or operator (same thing actually). Terminal nodes are constants or variables. A collection of programs is generated and the fitness of each is evaluated. In symbolic regression, fitness is typically the sum of the square difference between the function values and the data (lower values are more fit) or the data likelihood (higher values are more fit). A subset of the population is selected by fitness and genetic operators are applied. The genetic operators are operations such as crossover and mutation. In crossover, two trees are selected and selected branches from each of the trees are exchanged to produce new child trees. Mutation can change individual nodes or delete or add branches within a tree. Individuals with lower fitness are replaced by new individuals. The average fitness of the populations should increase as the algorithm proceeds. The choices of how to select individuals and how the operators are applied are the key elements for producing effective genetic programs.
Going DEAP
DEAP is a Python library for evolutionary computation. It supports a number of different data representations including trees for genetic programming and a number of different strategies for selection, mutation, and crossover of individuals.I decided to try DEAP on a toy problem. I generated some data from the following simple equation
\[y = {e^{ - 2.3x}}\cos (2\pi x) + \varepsilon \]
$\varepsilon \sim {\rm N}(0,0.05)$ represents the noise in the data. The data can be generated by
import numpy as np
x = np.arange(0.0, 3.0, 0.03)
y=np.exp(-2.3*x)*np.cos(2*math.pi*x)+np.random.normal(0, 0.05, size=len(x))
Here's what the data looks like

The green line is $y = {e^{ - 2.3x}}\cos (2\pi x)$
I'll try and fit this data by minimizing the sum of squared differences between the data and the predicted function.
\[\sum\limits_{i = 1}^N {{{\left( {f({x_i}) - {y_i}} \right)}^2}} \]
${f({x_i})}$ is the value of the function generated by the GP at $x_i$.
I tried a simple GP approach to finding a fit to this toy problem. Of course, if I know that it was generated from an exponential multiplied by a cosine, I could just fit the parameters with some sort of optimization routine. Instead, I'll use DEAP to try and fit the data.
DEAP has a number of modules for creation and manipulation of objects for genetic programming. To begin, the modules are imported.
from deap import algorithms
from deap import base
from deap import creator
from deap import tools
from deap import gp
The first thing DEAP requires is to set the operators and function you want the GP to use. We will want standard operators for +. -, *, and /. Since the data looks like it might have some sort of declining exponential and a wiggle, exponential and sinusoidal function would be useful. I realize I'm cheating because I know where the data came from.
Division and exponentiation cause problems because they can both have numerical difficulties. Instead of direct division and exponent functions, I use "safe" versions to avoid over and underflow.
def sDiv(left, right):
try:
res = left/right
except:
res = 1;
return res
def sexp(x):
try:
r = math.exp(x)
if r > 10:
r = 10
elif r < -10:
r = -10
except:
if x < 0:
r = -10
else:
r = 10
return r
pset = gp.PrimitiveSet("MAIN", 1)
pset.addPrimitive(operator.add, 2)
pset.addPrimitive(operator.sub, 2)
pset.addPrimitive(operator.mul, 2)
pset.addPrimitive(sDiv, 2)
pset.addPrimitive(operator.neg, 1)
pset.addPrimitive(math.cos, 1)
pset.addPrimitive(math.sin, 1)
pset.addPrimitive(sexp, 1)
pset.addEphemeralConstant("rand101", lambda: random.randint(-2,2))
pset.addEphemeralConstant("rand102", lambda: random.uniform(-3,3))
pset.renameArguments(ARG0='x')
pset stands for primitive set. It contains the basic operations and variables. for the genetic program. The addEphemeralConstant method allows the evolutionary algorithm to define constant values. renameArguments is syntactic sugar so that "x' is printed as a variable rather than some generated label like ARG0. I'm using a general except catchall for exception because I was having trouble catching specific exceptions from DEAP.
Next, DEAP expects some details about the objects we will be operating on. The code below creates an individual object type and describes the selection, mating, and mutation operations.
creator.create("FitnessMin", base.Fitness, weights=(-1.0,))
creator.create("Individual", gp.PrimitiveTree, fitness=creator.FitnessMin)
toolbox = base.Toolbox()
toolbox.register("expr", gp.genHalfAndHalf, pset=pset, min_=1, max_=2)
toolbox.register("individual", tools.initIterate, creator.Individual, toolbox.expr)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
toolbox.register("compile", gp.compile, pset=pset)
toolbox.register("select", tools.selTournament, tournsize=tourn_size)
toolbox.register("mate", gp.cxOnePoint)
toolbox.register("expr_mut", gp.genHalfAndHalf, min_=0, max_=2)
toolbox.register("mutate", gp.mutUniform, expr=toolbox.expr_mut, pset=pset)
genHalfAndHalf is an initialization operator. Half the time it creates an a tree where each leaf is at the same depth between min and max and the rest of the time the trees can have different heights. The population is a list of primitiveTrees. Selection is performed by a tournament. tourn_size individuals are randomly selected and the most fit individual is selected for a new generation. This process is repeated until a new population is created. Mating will be performed by crossover. A subtree is selected at random in each of two individual and the subtrees are exchanged between individuals. Mutation is accomplished by selecting a point in a tree and replacing it by a new subtree. DEAP provides a number of other selection, mutation, and initialization operators.
To get started, a population is created and the fitness of the initial population is evaluated.
pop = toolbox.population(n=pop_size)
fitnesses = [evalIndividual(individual, toolbox, x, y) for individual in pop]
for ind, fit in zip(pop, fitnesses):
ind.fitness.values = fit
The fitness criteria is the sum of the squares of the differences between an individual's tree evaluated at some point x and the value of the data at that point. The goal of the genetic program is to minimize this difference.
def evalFunc(func, xx):
res = []
for i in range(len(xx)):
try:
r = func(xx[i])
except:
r = 10
res.append(r)
return res
def evalIndividual(individual, toolbox, xx, yy):
func = toolbox.compile(expr=individual)
res = evalFunc(func, xx)
try:
sqerrors = sum((yy - np.array(res))**2)
if sqerrors > 100:
sqerrors = 100
except:
sqerrors = 100
return sqerrors,
The compile method compiles the tree into a function. evalFunc evaluates the function at each point and returns a list.
Once the initial population is created. for each generation a new set of offspring are created and then crossover and mutation operators are applied.
offspring = toolbox.select(pop, len(pop))
offspring = list(map(toolbox.clone, offspring))
for i in range(0, len(offspring), 2):
if np.random.random() < cxpb: # probability of applying crossover
toolbox.mate(offspring[i], offspring[i+1])
del offspring[i].fitness.values
del offspring[i+1].fitness.values
for i in range(len(offspring)):
if np.random.random() < mutpb: # probability of applying mutation
toolbox.mutate(offspring[i])
del offspring[i].fitness.values
invalid = [i for i in offspring if not i.fitness.valid]
fitnesses = [evalIndividual(individual, toolbox, x, y) for individual in invalid]
for ind, fit in zip(invalid, fitnesses):
ind.fitness.values = fit
pop[:] = offspring
Iterate for many generations and save the most fit individual over all generations.
best_in_pop = tools.selBest(pop, 1)
if best_in_pop[0].fitness.values[0] < best_fit:
best_fit = best_in_pop[0].fitness.values[0]
best_individual = best_in_pop[0]
That's it. You can get details of the various function at the DEAP website.
How well does it work?
The first thing I found out is that it takes a lot generations and several restarts to get a reasonable fit. The best fit had a sum of squared differences of 0.154. By contrast, the sum of squared differences between the green line and the data shown in the figure at the top is 0.295. The best fit individual is overfitting as can be seen in the figure. The red line is the fit from the genetic program and the green line is $y = {e^{ - 2.3x}}\cos (2\pi x)$.
Here's the generated function.
sDiv(mul(cos(sDiv(mul(mul(x, add(sub(cos(x), cos(sDiv(cos(cos(2)), sin(x)))), mul(cos(sub(sDiv(sDiv(neg(0.12084912071888843), cos(sin(sDiv(x, -0.6660501457462384)))), cos(sDiv(neg(sDiv(x, 1)), 1))), cos(sDiv(cos(mul(sDiv(x, -0.6660501457462384), sDiv(sDiv(sDiv(x, 1), cos(1.2208766195941578)), -0.4776167792855315))), mul(cos(1.8383603594526816), add(cos(sub(sDiv(x, -2.325902947790879), mul(x, x))), sub(cos(mul(2.4815364875941714, x)), 2.4815364875941714))))))), mul(mul(cos(sDiv(x, mul(cos(add(x, -1)), sub(x, 2.4815364875941714)))), mul(sDiv(-2.591707483553813, mul(sDiv(x, -0.6660501457462384), sDiv(sDiv(x, cos(sDiv(2.5453722898427715, 2.0823738927195503))), -0.4776167792855315))), cos(sDiv(sDiv(x, 0.34441264096461577), -0.4776167792855315)))), sub(x, sub(sin(sub(x, sub(sin(sDiv(x, cos(x))), x))), x)))))), -2.040730964037179), -0.4776167792855315)), mul(-0.0713284456494847, sDiv(1.1186438660288207, sub(sDiv(2.5453722898427715, 2.0823738927195503), sub(cos(sub(cos(-2), cos(sDiv(cos(sDiv(x, sub(sub(cos(add(x, sDiv(2.293956696850212, -2))), 2.4815364875941714), sDiv(-2, x)))), mul(cos(1.8383603594526816), add(add(cos(x), 0), sub(cos(sDiv(0, sub(x, 2.4815364875941714))), 2.4815364875941714))))))), sub(cos(sDiv(sDiv(sin(sDiv(sDiv(x, sexp(-2.7190559409962396)), -0.4776167792855315)), cos(sDiv(sDiv(add(sin(x), -1), cos(sDiv(2.5453722898427715, 2.0823738927195503))), -0.4776167792855315))), add(sin(sDiv(x, neg(x))), -1))), 2.4815364875941714)))))), x)
This result isn't especially satisfying. The fit is bad and it's unlikely that a human would come up with such a function or find it meaningful. We need some bloat control. Setting a limit on the size of the trees helps.
for i in range(0, len(offspring), 2):
if np.random.random() < cxpb:
old_child1 = copy.deepcopy(offspring[i])
old_child2 = copy.deepcopy(offspring[i+1])
toolbox.mate(offspring[i], offspring[i+1])
if offspring[i].height > max_height or offspring[i+1].height > max_height:
offspring[i] = copy.deepcopy(old_child1)
offspring[i+1] = copy.deepcopy(old_child2)
else:
del offspring[i].fitness.values
del offspring[i+1].fitness.values
for i in range(len(offspring)):
if np.random.random() < mutpb:
old_mutant = copy.deepcopy(offspring[i])
toolbox.mutate(offspring[i])
if offspring[i].height > max_height:
offspring[i] = copy.deepcopy(old_mutant)
else:
del offspring[i].fitness.values
A second problem that arises is that the solutions in any generation tend to form large niches, i.e. many individuals have the same structure and fitness. Setting a limit on the size of a niche improves the diversity of the population and helps prevent the algorithm from getting stuck.
def nicheSize(pop):
counts = defaultdict(int)
for individual in pop:
counts[str(individual)] += 1
max_key = max(counts.keys(), key=lambda k: counts[k])
return counts[max_key], max_key
def replaceNiche(pop, toolbox, max_niche_size):
counts = defaultdict(list)
for individual in pop:
counts[str(individual)].append(individual)
new_pop = []
for ind in counts:
if len(counts[ind]) > max_niche_size:
new_pop.extend(counts[ind][:max_niche_size])
replacements = toolbox.population(n=len(counts[ind]) - max_niche_size)
new_pop.extend(replacements)
else:
new_pop.extend(counts[ind])
return new_pop
niche_size = nicheSize(pop)
if niche_size > max_niche_size:
pop = replaceNiche(pop, toolbox, max_niche_size)
Limiting the tree size to six and the niche size to ten produces this fit with a sum of squares of 0.259.
Here's the equation of the red line. It's still complex.
sDiv(mul(sexp(mul(mul(neg(1.9564587657410835), add(x, x)), neg(-0.6358719041262324))), mul(cos(mul(add(2.068803256811913, 1), mul(-2.0819261756570517, x))), x)), mul(sexp(mul(sDiv(cos(x), mul(2.010875005950206, 2.2109953152893054)), mul(x, x))), sin(x)))
Here's what the tree looks like
Some the subrees can be consolidated. For example add(2.07, 1) can obviously be replaced by a node a single node 3.07.
This still isn't completely satisfying, but there are many other things to try including better mutation and selection operations (DEAP has a number of them) and running several populations in parallel. I could try adding a complexity or smoothness penalty to the fitness function.
DEAP has a number of complete algorithms that make programming genetic programs easier, but I wanted to be able to experiment and see the details.
The full source code and data is available here.




Comments
Post a Comment