In a previous post, I looked at the problem of combining the Bayesian Change Point algorithm with the Kalman filter. The results of applying the method to temperature anomaly data were less than spectacular.
With Bayesian change point algorithm, we assume that a change point represents a change in the marginalized probability of the data. There are other ways of thinking about what a change point means. A change point could be considered an anomaly or outlier in the data.
To get an idea of how outliers could be detected, consider a simple linear trend Kalman filter.
\[\begin{array}{l}{y_t} = {\theta _t} + {\upsilon _t}\,\,\,\,\,\,{\upsilon _t} \sim N(0,V)\\{\theta _t} = {\theta _{t - 1}} + {\omega _t}\,\,{\omega _t} \sim N(0,{W_t})\end{array}\]
In this model, we are assuming that the variances don't vary with time, but are drawn from some distribution, typically an inverse-gamma distribution.
\[{V_t} = \frac{1}{{{\phi _y}}}\,\,\,\,{W_t} = \frac{1}{{{\phi _\theta }}}\]
${\phi _y}$ and ${{\phi _\theta }}$ are priors drawn from a gamma distribution.
\[\begin{array}{l}{\phi _y} \sim G({\alpha _y},{\beta _y})\\{\phi _\theta } \sim G({\alpha _\theta },{\beta _\theta })\end{array}\]
${\alpha _y},{\beta _y}$, and ${\alpha _\theta }, {\beta _\theta }$ are hyperparameters. We will choose them weak enough so that they don't overwhelm the data.
Given the prior distributions, we can get the posterior distribution of these hyperparameters. I won't go through the derivation. You can find it in Dynamic Linear Models with R section 4.5.
\[\begin{array}{l}{\phi _y} \sim G\left( {{\alpha _y} + \frac{N}{2},{\beta _y} + \frac{1}{2}\left( {\sum\limits_{i = 1}^N {{{\left( {{y_t} - {\theta _t}} \right)}^2}} } \right)} \right)\\{\phi _\theta } \sim G\left( {{\alpha _\theta } + \frac{N}{2},{\beta _\theta } + \frac{1}{2}\left( {\sum\limits_{i = 1}^N {{{\left( {{\theta _t} - {\theta _{t - 1}}} \right)}^2}} } \right)} \right)\end{array}\]
A Kalman Filter Gibbs sampler
- Sample ${\phi _y}$ and ${\phi _\theta }$
- Run the Kalman Filter
- For i = N-1..1 sample ${{\theta _t}}$
#' kf_gibbs - Kalman Filter Gibbs sampler #' This is a simple tend following Kalman filter. It should be easy to adapt fpr more complicated models. #' Based on Dynamic Linear Models with R by Giovanni Petris . Sonia Petrone . Patrizia Campagnoli #' and the R dlm pacakage. #' #' @param df - A dataframe with columns Year and Temperature_Anomaly #' @param burnin - an int, Gibbs burnin period. #' @param samples - an int, Gibbs sampling period. #' @param C0 - an int, the variance of the pre-sample state vector. #' @param a1 - an int, parameter for gamma prior #' @param b1 - an int, parameter for gamma prior #' @param a2 - an int, parameter for gamma prior #' @param b2 - an int, parameter for gamma prior #' @param thin - an int, discard thin iterations for every saved iteration #' @param title - a string, option title for main plot. #' #' @return a list #' dlm - a dlm model (basically a list, see dlm pacakage docs) #' phi1, phi2 - saved inverse gamma draws #' df - a large dataframe, Year, Temperature_Anomaly from input df, posterior mean and sd of Kalman predictions, #' and draws for each iteration #' LL - the log likelihood for each iteration #' params - a list, input parameters #' #' @requires all int parameters >= 0 #' kf_gibbs <- function(df, burnin = 2000, samples = 10000, C0 = 1e+07, a1 = 2, b1 = 0.0001, a2 = 2, b2 = 0.0001, thin = 1, title = NULL) { require(tidyverse) require(ggpubr) require(dlm) # from Dynamic Linear Models with R b Giovanni Petris . Sonia Petrone . Patrizia Campagnoli # section 4.4.3 # starting values for posterior variance parameters phi1 <- 1 # 1/V phi2 <- 1 # 1/W # setup a dlm d <- dlmModPoly(order = 1, dV = 1 / phi1, dW = 1 / phi2, C0 = C0) iter_save = thin + 1 mc <- (burnin + samples) * iter_save #save parameter samples phi1_save <- numeric(burnin + samples) phi2_save <- numeric(burnin + samples) ll_save <- numeric(burnin + samples) # save log likelihood n <- nrow(df) # posterior params for inverse gamma sh1 <- a1 + n / 2 sh2 <- a2 + n / 2 df2 <- data.frame(Year = df$Year, Temperature_Anomaly = df$Temperature_Anomaly, posterior_mean = numeric(nrow(df)), sd = numeric(nrow(df))) save_count <- 1 # Gibbs sampler for(iter in 1:mc) { # show progress if(iter %% 100 == 0) { cat('Iteration ', iter, '\r') } # draw the states: FFBS filt <- dlmFilter(df2$Temperature_Anomaly, d) level <- dlmBSample(filt) if(iter %% iter_save == 0) { ll_save[save_count] <- dlmLL(df2$Temperature_Anomaly, d) # Save the samples df2 <- cbind(df2, level[-1]) names(df2)[ncol(df2)] <- paste0('sample_', save_count) } # draw observation precision phi1 rate <- b1 + crossprod(df$Temperature_Anomaly - level[-1]) / 2 phi1 <- rgamma(1, shape = sh1, rate = rate) # draw state precision phi2 rate <- b2 + crossprod(level[-1] - level[-n]) / 2 phi2 <- rgamma(1, shape = sh2, rate = rate) # update filter params V(d) <- 1 / phi1 W(d) <- 1 / phi2 if(iter %% iter_save == 0) { phi1_save[save_count] <- 1/phi1 phi2_save[save_count] <- 1/phi2 save_count <- save_count + 1 } } # posterior mean of sampled Kalman filter draws df2$posterior_mean <- rowMeans(df2[ , -(1:(burnin+4))]) df2$sd <- apply(df2[ , -(1:(burnin+4))], 1, sd) p <- ggplot(df2, aes(x = Year, y = Temperature_Anomaly, color = 'Temperature Anomaly')) + geom_point() + # geom_line() + geom_point(aes(x = Year, y = posterior_mean, color = 'Posterior Mean')) + geom_line(aes(x = Year, y = posterior_mean, color = 'Posterior Mean')) + geom_ribbon(aes(x = Year, y = posterior_mean, ymin = posterior_mean - sd, ymax = posterior_mean + sd, color = '+/- SD'), fill = 'grey', alpha = 0.4) + ylab('Temperature Anomaly') + scale_colour_manual(name = '', values = c('grey', 'seagreen', 'brown')) if(! is.null(title)) { p <- p + ggtitle(title) } print(p) # plot sampled variances df3 <- data.frame(Iteration = (burnin+1):(mc/iter_save), phi1 = phi1_save[-(1:burnin)], phi2 = phi2_save[-(1:burnin)]) p2 <- ggplot(df3, aes(x = Iteration, y = phi1)) + geom_line() + ylab(expression(phi[y])) + ggtitle(expression(phi[y])) p3 <- ggplot(df3, aes(x = Iteration, y = phi2)) + geom_line() + ylab(expression(phi[theta])) + ggtitle(expression(phi[theta])) p4 <- ggarrange(plotlist = list(p2, p3), ncol = 1, nrow = 2) print(p4) return(list(dlm = d, phi1 = phi1_save, phi2 = phi2_save, df = df2, LL = ll_save, params = list(a1 = a1 , b1 = b1, a2 = a2, b2 = b2, burnin = burnin, samples = samples, thin = thin, title = title))) }
Outliers
#' kf_gibbs_t - Gibbs sampler for Kalman filter #' Assumes a heavy-tailed distribution (Student t) for variances rather than the normal distribution #' Described in Chapter 4 of Dynamic Linear Models with R by Giovanni Petris . Sonia Petrone . Patrizia Campagnoli #' #' @param df - A dataframe with columns Year and Temperature_Anomaly #' @param mod - A dlm model. #' @param A_y - numerical, Prior mean for observational precision. #' @param B_y - numerical, Prior mean for observational variance. #' @param A_theta - numerical, Prior mean for system precision. #' @param B_theta - numerical, Prior mean for system variance. #' @param burnin - an int, Gibbs burnin period. #' @param samples - an int, Gibbs sampling period. #' @param save_states - logical, Should sampled states be saved? #' @param thin - an int, Discard thin iterations for every saved iteration? #' @param cutoff - Values of omega_theta <= cutoff are considere outliers. #' @param title - Optional title for model plot. #' #' @return - a list #' d: a dlm, output of dlmGibbsDIGt, #' df2: a dataframe, with Year, Temperature_Anomaly, omega_y, omega_theta, posterior mean of samples and #' sd of damples = df2, outliers = outliers. #' outliers: index of outlier rows in dataframe #' params - a list, input parameters #' #' @requires - cutoff <= 1, #' dlmGibbsDIGt from https://www.jstatsoft.org/index.php/jss/article/downloadSuppFile/v036i12/dlmGibbsDIGt.R #' kf_gibbs_t <- function(df, mod = dlmModPoly(1), A_y = 1, B_y = 1, A_theta = 10, B_theta = 10, burnin = 2000, samples = 10000, save_states = TRUE, thin = 1, cutoff = 0.95, title = NULL) { require(dlm) require(tidyverse) require(ggpubr) # use dlmGibbsDIGt from https://www.jstatsoft.org/index.php/jss/article/downloadSuppFile/v036i12/dlmGibbsDIGt.R # to do the heavy lifting. # See Dynamic Linear Models with R section 4.5.3 for details d <- dlmGibbsDIGt(df$Temperature_Anomaly, mod = mod, A_y = A_y, B_y = B_y, A_theta = A_theta, B_theta = B_theta, n.sample = burnin + samples, thin = thin, save.states = save_states) # get the posterion mean and sd of latent variables, omegas df2 <- data.frame(Year = df$Year, Temperature_Anomaly = df$Temperature_Anomaly, omega_y = colMeans(d$omega_y[-(1:burnin), ]), omega_theta = rowMeans(d$omega_theta[, 1, -(1:burnin)])) outliers <- which(df2$omega_theta <= cutoff) # these are positions with large variance in predicted mean if(save_states) { # get posterior mean and sd of the Kalman filter predictions and plot them df2 <- cbind(df2, data.frame(Posterior_Mean = rowMeans(d$theta[-1, 1, -(1:burnin)]), sd = apply(d$theta[-1, 1, -(1:burnin)], 1, sd))) p1 <- ggplot(df2) + geom_point(aes(x = Year, y = Temperature_Anomaly, color = 'Temperature Anomaly')) + geom_line(aes(x = Year, y = Posterior_Mean, color = 'Posterior Mean')) + geom_point(aes(x = Year, y = Posterior_Mean, color = 'Posterior Mean')) + geom_ribbon(aes(x = Year, y = Posterior_Mean, ymin = Posterior_Mean - sd, ymax = Posterior_Mean + sd, color = '+/- SD'), fill = 'grey', alpha = 0.4) + geom_point(data = data.frame(Year = df2$Year[outliers], Temperature_Anomaly = df2$Temperature_Anomaly[outliers]), aes(x = Year, y = Temperature_Anomaly, color = 'Outliers')) + ylab('Temperature Anomaly') + scale_colour_manual(name = '', labels = c('+/- SD', expression(paste('Outliers ', omega[theta])), 'Posterior Mean', 'Temperature Anomaly'), values = c('grey', 'red', 'seagreen', 'blue')) if(! is.null(title)) { p1 <- p1 + ggtitle(title) } print(p1) } # plot the latent variables p2 <- ggplot(df2) + geom_point(aes(x = Year, y = omega_y)) + geom_hline(yintercept = 1) + ylab(expression(omega[y])) p3 <- ggplot(df2) + geom_point(aes(x = Year, y = omega_theta)) + geom_hline(yintercept = 1) + geom_hline(yintercept = cutoff, color = 'red') + ylab(expression(omega[theta])) p4 <- ggarrange(plotlist = list(p2, p3), nrow = 2, ncol = 1) print(p4) return(list(d = d, df2 = df2, outliers = outliers, params = list(mod = mod, A_y = A_y, B_y = B_y, A_theta = A_theta, B_theta = B_theta, burnin = burnin, samples = samples, save_states = save_states, thin = thin, cutoff = cutoff, title = title))) }
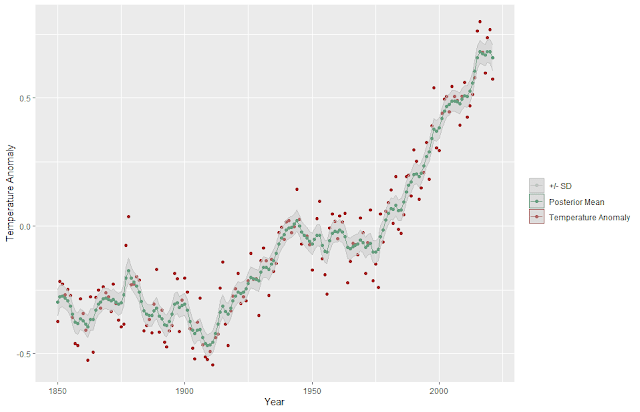
The outliers in the trend, shown in red may indicate some shift in the underlying process generating the data points.




No comments:
Post a Comment